Un límite en matemáticas es el valor al que se acerca una función (o secuencia) a medida que la entrada (o índice) se acerca a un cierto punto. El límite nos ayuda a comprender cómo se comporta una función cerca de un punto específico. Desempeña un papel básico en la definición de continuidad, derivación e integración.
GH Hardy introdujo la notación con la flecha debajo del símbolo de límite, «→» en su libro de 1908, «Un curso de matemáticas puras». Esta notación se utiliza ahora ampliamente para representar límites en matemáticas.
Este artículo cubrirá definiciones, tipos y propiedades de límites. También proporcionará orientación sobre la resolución de problemas de límites e incluirá una sección con varios ejemplos para una mejor comprensión.
Definición y notación de un límite.
El límite representa el valor al que se acerca la función o secuencia a medida que su entrada se acerca arbitrariamente a un determinado valor. Considere f(x) como una función real, x se acerca a un número real c y una función f(x) se acerca a un número particular L , entonces se dice que L es el límite de una función dada. La notación matemática del límite es:
Lim x → cf (x) = L
Definición formal de límite
Supongamos que f es una función y c es cualquier número real. Decimos que el límite de f(x) cuando x se aproxima a c es L si, para cada ε > 0, existe un δ > 0 tal que 0 < |x – c| < δ entonces |f(x) – L| <ε.
Tipos de límite
En el cálculo están presentes muchos tipos de límites, pero los que se describen aquí son los que se observan con mayor frecuencia.
Límite unilateral (o límite unilateral)
Un límite unilateral se refiere al límite de una función cuando la entrada se acerca a un punto específico desde una sola dirección, ya sea desde la izquierda o desde la derecha. Nos ayuda a comprender el comportamiento de la función en un lado del punto. Observó que:
- lim x → c + f(x) = L (para límite del lado derecho)
- lim x → c – f(x) = L (para límite del lado izquierdo)
Límite bilateral (o límite bilateral)
El límite bilateral es el límite de una función cuando la entrada se acerca a un punto específico c desde el lado izquierdo y derecho simultáneamente. Representa el comportamiento de la función alrededor de c sin distinguir entre las direcciones izquierda y derecha.
Matemáticamente, el límite bilateral se expresa como:
lím x → c f(x) = L
Límite infinito
Un límite infinito ocurre cuando la función se acerca al infinito positivo o negativo a medida que la entrada se acerca arbitrariamente a un punto particular. Esto indica que la función crece sin límite o disminuye sin límite a medida que se acerca al punto especificado.
Un límite infinito se puede escribir como :
- límite x → C f (x) = + ∞ (Para un límite que llega al infinito positivo)
- límite x → C f (x) = – ∞ (Para un límite que llega al infinito negativo)
Límite en el infinito
El límite en el infinito representa el comportamiento de una función cuando la entrada se vuelve extremadamente grande (positiva o negativa). Nos ayuda a comprender a qué se acerca la función cuando ‘x’ se mueve hacia el infinito o el infinito negativo.
- límite x → ∞ f(x) (para un límite cuando ‘x’ se acerca al infinito positivo)
- lím x → – ∞ f(x) (para un límite cuando ‘x’ se acerca al infinito negativo)
Propiedades del límite
A continuación se muestran algunas propiedades y reglas asociadas con los límites:
Sea lím x → C f (x) y lím x → C g(x) existe y k es cualquier constante. Entonces,
- límite x → C k = k
Un límite de la constante es lo mismo que la constante misma.
- Lim x → c [f(x) ± g(x)] = límite x → c f(x) ± lím x → c g(x)
El límite de la suma o diferencia de dos funciones es igual a la suma o diferencia de sus límites.
- lim x → c [f(x) × g(x)] = lim x → c f(x) × lim x → c g(x)
El límite del producto de dos funciones es igual al producto de sus límites.
- Lim x → c [f(x) / g(x)] = [lim x → c f(x) / lím x → c g(x)]
El límite del cociente de dos funciones es igual al cociente de sus límites, siempre que el límite del denominador no sea cero.
- lim x → c (kg(x)) = k lim x → c g(x)
De un límite se puede extraer un factor constante .
- lim x → c (g(x)) n = (lim x → c g(x)) n
El límite de una función elevada a la potencia de n es igual a la n- ésima potencia del límite de la función.
- lím x → c xk = ck
Ejemplos resueltos de límite
A continuación se muestran algunos ejemplos resueltos de límites para ayudar a solidificar el concepto de límite.
Ejemplo 1:
Evaluar lím x → – 2 (4x 2 + 9x – 4)
Solución:
Podemos dividir el límite en tres límites separados usando una propiedad de límites. Luego, usaremos otra propiedad para sacar constantes de los dos primeros límites. Esto nos da lo siguiente:
lím x → – 2 (4x 2 + 9x 2 – 4) = lím x → – 2 (4x 2 ) + lím x → – 2 (9x) – lím x → – 2 (4)
= 4 lím x → – 2 (x 2 ) + 9 lím x → – 2 (x) – 4 lím x → – 2 (1)
= 4 (– 2) 2 + 9(– 2) – 4 (1)
= 16 – 18 – 4
= – 6
Se puede utilizar un buscador de límites para calcular límites de funciones y deshacerse de los cálculos manuales.
Ejemplo 2:
Calcule el siguiente límite.
![]()
Solución:
Dado
![]()
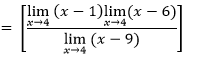
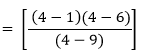
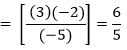
Ejemplo 3:
Evaluar
![]()
Solución:
Dado
![]()
El numerador y el denominador de la función se convertirán en 0 si sustituimos el valor 1 directamente en la función, lo que dará como resultado una forma indeterminada de 0/0. Se puede encontrar una expresión simplificada usando la propiedad de los cuadrados.
![]()
= lím x → 1 (x + 1)
= 2
Conclusión
En este artículo, hemos explorado el concepto de límites en matemáticas. Discutimos la definición formal de un límite, incluida la definición épsilon-delta, y varios tipos de límites. Cubrimos propiedades y reglas de límites que son cruciales para simplificar los cálculos de límites. El artículo también proporciona ejemplos para ilustrar cómo calcular límites en la práctica. Después de leer este artículo podrás solucionar cualquier problema relacionado con el límite.