El cálculo es una rama fundamental de las matemáticas que ha revolucionado la forma en que entendemos el cambio y el movimiento en el mundo que nos rodea. Una de las herramientas más poderosas en el cálculo es el concepto de derivadas. Para comprender y aplicar adecuadamente las derivadas, es esencial conocer el principio subyacente para calcularlas.
En este artículo, exploraremos en detalle el principio para calcular derivadas, su importancia en diversos campos y cómo utilizarlo de manera efectiva. Si estás emocionado por aprender y mejorar tus habilidades en cálculo, además de que es importante que conozcas la Derivada Parcial En Symbolab, ¡vamos a sumergirnos en el fascinante mundo de las derivadas!
¿Qué son las Derivadas?
Las derivadas son una de las piedras angulares del cálculo y se utilizan para medir cómo una función cambia en relación con su variable independiente. Matemáticamente, la derivada de una función f(x) en un punto dado x₀ se denota como f'(x₀) o dy/dx. Representa la tasa de cambio instantáneo de la función en ese punto específico. En otras palabras, las derivadas nos permiten analizar la pendiente o inclinación de una curva en un punto particular, lo que es esencial para comprender cómo varían las cantidades en función de otras.
Importancia del Cálculo y las Derivadas
El cálculo y, por extensión, las derivadas, son esenciales en una amplia gama de disciplinas, incluyendo:
1. Física
En física, las derivadas son vitales para describir el movimiento de objetos y analizar conceptos como velocidad, aceleración y fuerza. Las leyes del movimiento de Newton y otras teorías fundamentales se expresan a través de ecuaciones diferenciales que involucran derivadas.
2. Economía
El cálculo y las derivadas son herramientas cruciales en economía para modelar el crecimiento económico, optimizar la producción y analizar el comportamiento de los mercados financieros.
3. Ingeniería
En ingeniería, las derivadas se utilizan para diseñar y analizar sistemas complejos, como circuitos eléctricos, estructuras y sistemas de control automático.
4. Ciencias de la Computación
En ciencias de la computación, las derivadas son fundamentales para el diseño de algoritmos y la optimización de procesos, como la búsqueda en inteligencia artificial y el análisis de datos.
Principio para Calcular Derivadas
El principio fundamental para calcular derivadas es el conocido como «Regla del límite de la pendiente de la tangente». Esta regla establece que la derivada de una función f(x) en un punto x₀ es igual a la pendiente de la recta tangente a la curva de la función en ese punto. Formalmente, esta regla se expresa como:
1. Derivada de una Función Constante
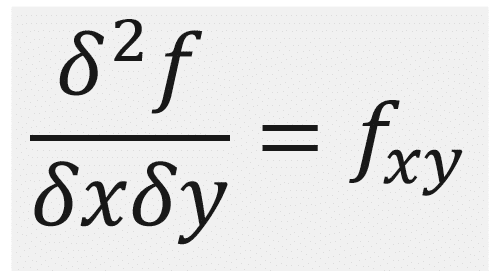
Para calcular la derivada de una función constante, simplemente aplicamos la regla del límite. Sea f(x) = c, donde c es una constante, entonces:
2. Derivada de una Función Potencia
La derivada de una función potencia f(x) = xⁿ, donde n es un número real, puede calcularse utilizando la regla del límite. El resultado es:
3. Derivada de una Función Exponencial
Para calcular la derivada de una función exponencial f(x) = e^x, donde e es la base del logaritmo natural, podemos aplicar nuevamente la regla del límite. El resultado es:
4. Derivada de una Función Logarítmica
La derivada de una función logarítmica f(x) = ln(x) también se puede encontrar mediante la regla del límite. El resultado es:
5. Derivada de una Suma o Resta de Funciones
Cuando tenemos una función compuesta por la suma o resta de dos o más funciones, podemos encontrar su derivada aplicando la regla del límite a cada función individualmente. Luego, simplemente sumamos o restamos las derivadas obtenidas.
6. Derivada de un Producto de Funciones
Para hallar la derivada de una función que es el producto de dos funciones, utilizamos la regla del límite y la regla del producto. El resultado es:
7. Derivada de un Cociente de Funciones
Cuando nos enfrentamos a una función que es el cociente de dos funciones, podemos encontrar su derivada aplicando la regla del límite y la regla del cociente. El resultado es:
8. Derivada de una Función Compuesta
La derivada de una función compuesta f(g(x)) se puede calcular utilizando la regla de la cadena, que nos permite relacionar las derivadas de ambas funciones. El resultado es:
9. Derivadas de Funciones Trigonométricas
Las derivadas de las funciones trigonométricas (seno, coseno, tangente, cotangente, secante y cosecante) se pueden encontrar aplicando la regla del límite y las derivadas de las funciones trigonométricas básicas.
10. Derivada de una Función Inversa
Para calcular la derivada de una función inversa f⁻¹(x), podemos utilizar la regla del límite y la relación entre las derivadas de la función original y su función inversa.
11. Derivadas Implícitas
Cuando tenemos una ecuación implícita que define una función, podemos encontrar su derivada implícita aplicando la regla del límite y derivando cada término respecto a la variable dependiente.

12. Derivadas de Funciones Paramétricas
Las derivadas de funciones paramétricas x = f(t) e y = g(t) se pueden calcular mediante la regla del límite y las derivadas de las funciones f(t) y g(t) respecto a t.
13. Derivada Direccional
La derivada direccional nos permite medir la tasa de cambio de una función en una dirección específica. Se calcula utilizando el gradiente de la función y un vector unitario que indica la dirección.
14. Derivadas Parciales
Cuando tenemos una función de varias variables, podemos calcular sus derivadas parciales respecto a cada variable individualmente, manteniendo las demás constantes.
15. Derivadas Numéricas
En casos donde no sea posible obtener la derivada analítica de una función, las derivadas numéricas proporcionan una aproximación mediante la aplicación de métodos numéricos, como el método de diferencias finitas.
16. Aplicaciones de las Derivadas
Las aplicaciones de las derivadas son extensas y abarcan diversas áreas de la ciencia y la ingeniería. Algunos ejemplos notables incluyen:
- Optimización: Encontrar máximos y mínimos de funciones, lo cual es útil en economía y ciencias de la computación.
- Modelado de Sistemas Dinámicos: En física y biología, las derivadas ayudan a modelar el comportamiento de sistemas complejos a lo largo del tiempo.
- Análisis de Circuitos: En ingeniería eléctrica, las derivadas se utilizan para analizar circuitos y sistemas eléctricos.
- Predicción de Tendencias: En análisis de datos, las derivadas permiten predecir tendencias y patrones en grandes conjuntos de datos.
- Geometría Diferencial: En matemáticas avanzadas, las derivadas son fundamentales para estudiar las propiedades geométricas de curvas y superficies.
17. Ejemplos Prácticos
Para comprender mejor cómo calcular derivadas y aplicar el principio en diferentes contextos, consideremos algunos ejemplos prácticos:
- Calculando la velocidad de un objeto en un punto específico durante su movimiento.
- Encontrando el punto en el que la pendiente de una curva es máxima o mínima.
- Modelando el crecimiento de una población en función del tiempo.
- Analizando la velocidad y aceleración de un vehículo en movimiento.
- Optimizando la producción de una empresa para maximizar las ganancias.
Conoce el principio para calcular derivadas
Sin duda, el principio para calcular derivadas es uno de los fundamentos más esenciales del cálculo y tiene aplicaciones extensas en diversas áreas del conocimiento. Al dominar este principio, puedes obtener una comprensión más profunda del cambio y el movimiento en el mundo que te rodea, lo que te permitirá abordar problemas complejos con mayor eficacia. A través de ejemplos prácticos y la comprensión de las reglas clave, estarás listo para enfrentar desafíos matemáticos y científicos con confianza.

FAQs sobre el principio para calcular derivadas
¿Qué es una derivada y para qué se utiliza?
Una derivada es una medida de cómo una función cambia en relación con su variable independiente. Se utiliza para analizar la tasa de cambio instantáneo de una función en un punto específico y tiene aplicaciones en física, economía, ingeniería, ciencias de la computación y más.
¿Cómo se calcula la derivada de una función constante?
La derivada de una función constante es siempre cero, ya que no cambia con respecto a su variable independiente. Matemáticamente, si f(x) = c, donde c es una constante, entonces f'(x) = 0.
¿Cuál es el principio fundamental para calcular derivadas?
El principio fundamental para calcular derivadas es la «Regla del límite de la pendiente de la tangente». Esta regla establece que la derivada de una función en un punto dado es igual a la pendiente de la recta tangente a la curva de la función en ese punto.
¿Cuál es la importancia de las derivadas en la física?
En física, las derivadas son fundamentales para describir el movimiento de objetos y analizar conceptos como velocidad, aceleración y fuerza. Las leyes del movimiento de Newton y otras teorías clave se expresan mediante ecuaciones diferenciales que involucran derivadas.
¿Cómo se encuentran las derivadas de funciones trigonométricas?
Las derivadas de las funciones trigonométricas (seno, coseno, tangente, cotangente, secante y cosecante) se pueden encontrar aplicando la regla del límite y las derivadas de las funciones trigonométricas básicas.
¿Cuál es la utilidad de las derivadas numéricas?
Las derivadas numéricas proporcionan una aproximación de la derivada de una función en puntos específicos mediante métodos numéricos, lo que es útil cuando no se puede obtener una derivada analítica de la función.
¿En qué campos se aplican las derivadas?
Las derivadas tienen aplicaciones extensas en física, economía, ingeniería, ciencias de la computación, análisis de datos, modelado de sistemas dinámicos, geometría diferencial y más.
Conclusión: Conoce el principio para calcular derivadas
El principio para calcular derivadas es esencial para comprender y aplicar el cálculo en diversos campos científicos y de ingeniería. Desde la física hasta la economía y la ciencia de datos, las derivadas desempeñan un papel fundamental en el análisis del cambio y la optimización de sistemas complejos. Mediante ejemplos prácticos y la comprensión de las reglas clave, esperamos que este artículo te haya brindado una visión completa y detallada sobre cómo calcular derivadas y su importancia en el mundo moderno.
Recuerda que el cálculo es una herramienta poderosa que ha permitido a la humanidad avanzar en el conocimiento y el desarrollo tecnológico. ¡Así que sigue explorando y aplicando estos principios matemáticos en tu vida diaria y en tus investigaciones científicas para marcar la diferencia!