Principio de Bernoulli

El estudio del comportamiento se puede realizar utilizando conceptos de la física de fluidos. El principio de Bernoulli o ecuación de Bernoulli es uno de los teoremas más aplicados que se encuentra en esta área. El científico suizo Daniel Bernoulli expuso este postulado dentro de su publicación “Hidrodinámica”, y explica el movimiento de líquidos a través de un conducto cerrado.

De manera más extensa, este principio es definido como el comportamiento que presenta un fluido a medida que este se moviliza a través de una línea de corriente. Además, se entiende que el líquido debe ser considerado ideal siempre que cumpla dos características durante su circulación dentro del conducto cerrado: no existe viscosidad ni rozamiento. Es así como la energía de este permanecerá siempre constante.

La aplicación del principio de Bernoulli ha sido posible en distintas áreas. Desde la construcción hasta la mecánica, pudiendo obtener resultados prometedores y funcionales.  A través del mismo, se han podido resolver distintos problemas del universo, pudiendo dar respuesta a incógnitas en torno a este.

¿Qué es el principio de Bernoulli?

Dentro del principio de Bernoulli se describe la manera en que se comporta un fluido al moverse dentro de una línea de corriente. Se establece que se considera que es un fluido ideal cuando carece de viscosidad y no existe rozamiento mientras este transita en un conducto cerrado, manteniendo la energía constante a lo largo de su recorrido.

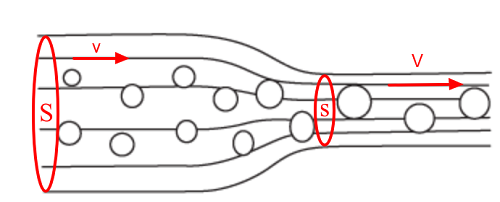
Otra de las premisas que se establece en el enunciado, declara que el líquido que se encuentra dentro de un flujo horizontal tendrá mayor velocidad en los puntos donde exista menor presión, mientras que donde exista mayor presión, la velocidad será menor. Por lo que, si un conducto cambia su diámetro en determinadas zonas, ocurrirá una variación en la velocidad con que se mueve el fluido.

Pero la ecuación de Bernoulli puede ser aplicable en distintos tipos de flujo, tanto en líquidos como en gases. Esto permite obtener varias formas de la ecuación. En caso de tratarse de un flujo incomprensible, se puede aplicar la forma básica de la ecuación, siempre que el movimiento sea en un bajo número Mach. En el caso en que se trate de números altos de Mach, entonces se utilizará una forma más compleja de la ecuación.

Ecuación de flujo incomprensible

Los fluidos incompresibles se destacan por poseer un número Mach bajo, por lo que sin importar si se mueven a través de zonas estrechas, aumentan la velocidad para mantener un flujo constante. Es así como son considerados dentro del flujo incomprensible. Pero antes de definir la ecuación, se tiene en cuenta los tres componentes de la energía de un fluido:

• Energía cinética: se relaciona con la velocidad a la que se mueve el fluido.
• Energía potencial: energía producto de la altitud que posee el fluido.
• Energía de presión: energía resultante de la presión que posee el fluido.

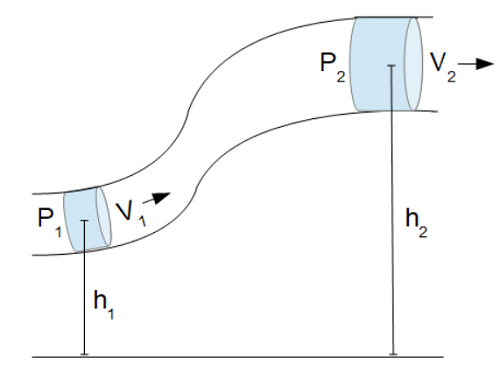
Así mismo, se tiene que estos fluidos solo se estudian a través de la ecuación básica de Bernoulli, que comprende:

Definiendo cada una de las variables de la siguiente manera:

• V= velocidad del fluido cuando se mueve a través de una sección determinada.
• ρ= densidad del fluido.
• P= presión del fluido a lo largo del conducto que recorre.
• g= aceleración gravitatoria.
• z= altura en dirección de la gravedad tomando en cuenta la elevación desde en un determinado.

Pero para lograr aplicarla correctamente, también se debe tomar en cuenta otros factores:

• No debe existir viscosidad dentro de la línea de corriente.
• El caudal debe ser constante.
• Al tratarse de un flujo incomprensible, p debe ser constante.
• Es aplicable en una línea de corriente o un flujo laminar.

Esta misma ecuación se puede utilizar para trabajar con gases. Pero para que sea posible, es necesario que el balance energético no varíe. En otras palabras, no se puede trabajar sobre el gas. Además, se debe tener en cuenta que la transferencia de calor debe ser igual a cero, cumpliéndose en ciclos termodinámico completo e isoentrópico, en los cuales no existe fricción y son adiabáticos. Además, el flujo de gas está por debajo de la velocidad del sonido y el flojo adiabático en Mach es menor a 0.3.

Ecuación de flujo comprensible

Mediante la observación del comportamiento de los líquidos, Bernoulli pudo determinar que es posible aplicar la ecuación en fluidos comprensibles e incompresibles, pero solo hasta el número 0.3 de Mach. Para valores más elevados, es necesario utilizar otros principios pertenecientes a la física para desarrollar ecuaciones más complejas. Esto permitirá resolver problemas de fluidos bajo el principio de Bernoulli.

Flujo comprensible en dinámica de fluidos

En este caso, la ecuación de Bernoulli se trabaja combinada con la ecuación de estado barotrópica y mientras se encuentre bajo la acción de fuerzas conservadoras. De esta manera se obtiene la siguiente fórmula:

Definiendo las variables:

• p = hace referencia a la presión.
• ρ= es la densidad, mientras que es la función de la presión.
• v= es la velocidad de flujo
• Ψ= se conoce como el potencial gravitatorio.

Pero si se está trabajando con un gas que se considera ideal, la ecuación varía:

Siendo las variables:

• ƴ= es la relación entre los calores específicos del fluido.
• g= aceleración producto de la gravedad.
• z= elevación de un punto en una región determinada.

En caso de que la elevación sea considerada insignificante, entonces gz puede ignorarse, teniendo:

p₀ se conoce como la presión inicial, y ρ₀ la densidad inicial del proceso.

Flujo comprensible en termodinámica

Es posible aplicar dos ecuaciones. Si el flujo es casi constante, entonces:

, donde w es la entalpía específica.

Si se ignora el cambio, al permanecer constante, entonces se obtiene:

, donde w₀ es la entalpía total.

Aplicación del principio de Bernoulli

De manera cotidiana podemos encontrar ejemplos de la aplicación del principio de Bernoulli. Ha sido de gran ayuda para la elaboración de distintos objetos que utilizamos regularmente, pudiendo resolver algunos problemas en su funcionamiento:

• Las chimeneas: es fácil notar que estas son altas. La razón es para aprovechar la que la velocidad del viento es más constante a mayor altura. Si el viento sopla rápido sobre la boca de la chimenea, entonces la presión será más baja. Esto aumenta la diferencia de presiones entre la boca y base de la chimenea, lo que facilita el flujo de gases a través de esta.
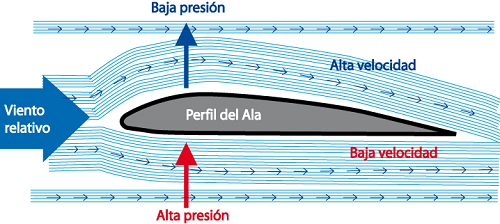
• Los aviones: la aviación ha utilizado esta ecuación para lograr que los aviones puedan volar. La parte superior del ala ha sido diseñada más curva que la parte inferior. En el momento en que la masa superior de aire aumente su velocidad, la presión disminuye. Esto es lo que permite que el avión se mantenga en el aire.
• La natación: Al momento en que se realizan las brazadas, se corta el agua. En ese instante disminuye la presión, y el cuerpo adquiere mayor propulsión.

Si quieres saber más te recomendamos visitar el siguienet curso.